金沢大学附属中学受験や入試 について
詳しくはこちら
金沢大学附属中学を受験する子たちはもらったかな?
令和6年度の受験問題。
今の中学1年生が受験した時の問題です。
ちょっと分かりにくい問題をブログで解説しますね。
著作権が厳しい国語は難しいので、算数を中心にします。
では、今日は大問6について解説します。
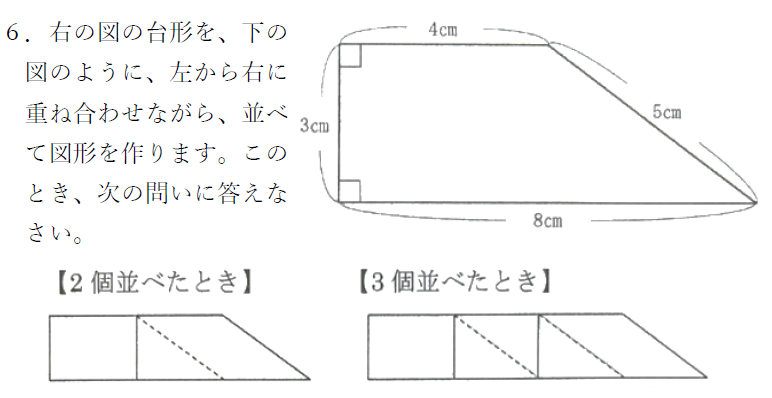
(1)台形を4個並べてできる図形の面積は何㎠ですか。
(2)できた図形の周りの長さが284cmのとき、台形はいくつ並べましたか。
まだ解いていない子は、ここで一旦ストップして解いてみましょう。
下にスクロールしたら答えになります。
では、答えと解説を書きます。
(1)
台形を4個並べると、横長の台形が出来ます。
上の図の2個のときと3個のときをご覧ください。
2個のときの上底は4×2=8cm
3個のときの上底は4×3=12cm
なので4個並べたときの上底は
4×4=16cm となります。
2個のときの下底は4×3=12cm
3個のときの下底は4×4=16cm
なので4個並べたときの下底は
4×5=20cm となります。
高さは常に3cmです。
よって4個並べてできる図形の面積は
(16+20)×3÷2 = 54㎠ となります。
(2)
同じく上の2個と3個の図をご覧ください。
上底と下底だけが伸びています。
高さと右部の斜め線の部分は増えていません。
つまり、台形が1個増えるにつれ、上底と下底合わせて8cmずつ伸びていきます。
台形1個のときの周の長さは 20cm。
今求める図形の周りの長さは 284cm。
264cm伸びました。
つまり
264÷8=33回 伸びたことが分かります。
1個目から33回伸びたわけです。
ですから並べた台形の個数は、最初の1個を合わせ
1+33 = 34個並べた ということになります。
数の規則性の問題です。
令和6年度は等差数列と植木算を使いました。
令和5年度は図形の周期を見て考える問題でした。
等差数列・植木算・周期算あたりが金沢大学附属中学入試の好みなのでしょうか。
8~12点分ほど出ますので、やっておきましょう。


コメント